３－３．FFTスペクトルの定量性について


　片振幅１の正弦波をフーリエ変換した時の振幅スペクトルのピークは１になるはずですが、次のような条件が必要です。

・演算窓の右端と左端の位相が同じになる。
・窓関数を使わない。（窓関数　BOX)
・ゼロ補間を使わない。
box1
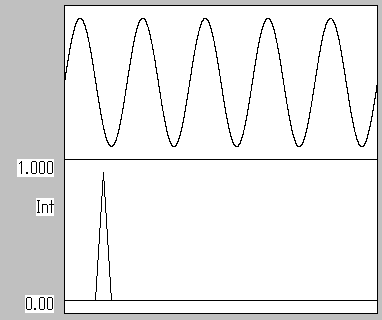
窓関数 BOX 左端と右端の位相差０　ピーク高さは１になる

　演算窓の左端と右端の位相が異なると下記の図のように、ピークは１より小さい値になります。
　また、ピークの形も歪んでいます。
box2
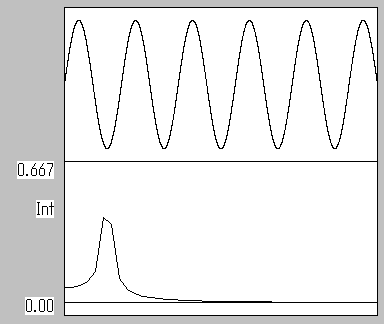
窓関数 BOX 左端と右端の位相差 180　ピーク高さは0.667になる。

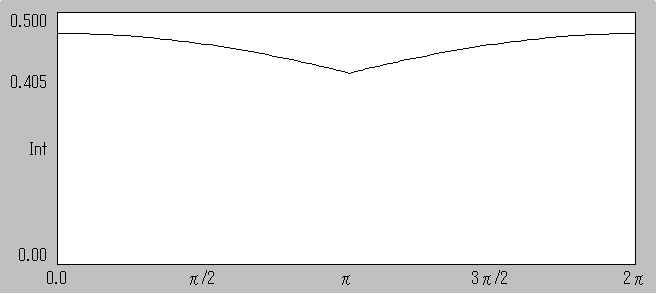
　窓関数HANNINGを使うとピーク高さは下記のように1/2になります。
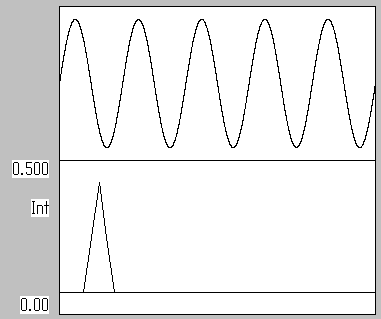
hanning1
窓関数 HANNING 左端と右端の位相差０　ピーク高さは0.5になる

　窓関数HANNING を使うと図のように左端と右端の位相差 がある場合でもピークの落ち込みが少なくなります。
　ピークの歪みもましになります。
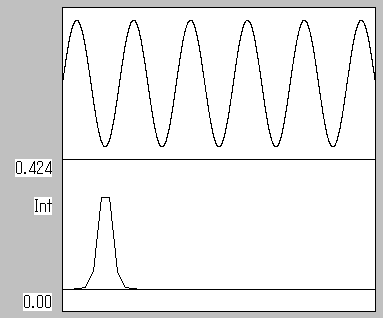
hanning2
窓関数 HANNING 左端と右端の位相差 180　ピーク高さは0.424になる

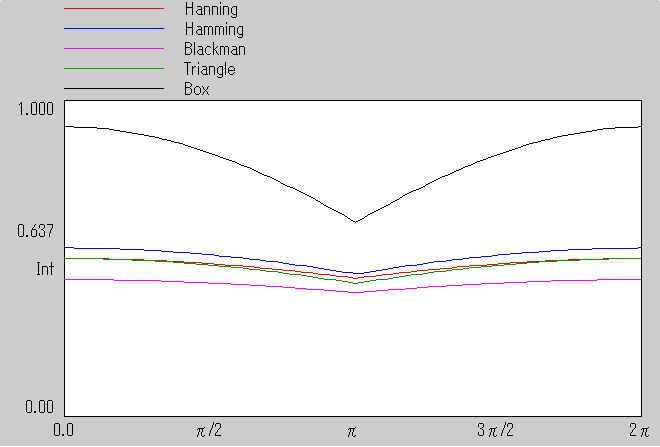
演算窓の左端と右端の位相差とピークの高さの関係は下記のグラフのようになります。
窓関数 BOX の場合　ピークの最大値を100%とすると最小値は 63.7%となります。
box

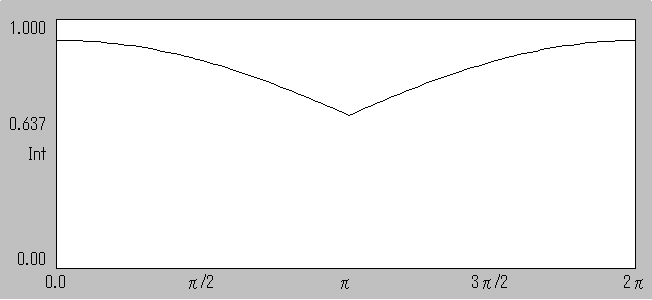
窓関数 HANNING の場合　ピークの最大値を100%とすると最小値は 84.8%となります。
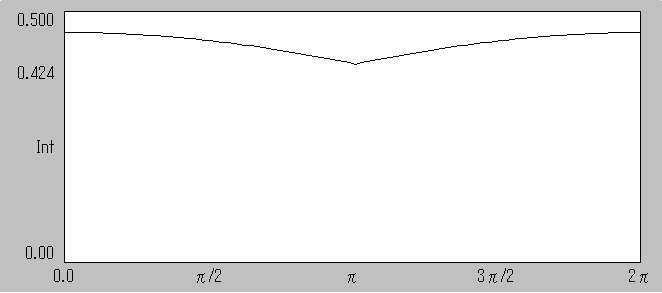
hanning

窓関数 HAMMING の場合　ピークの最大値を100%とすると最小値は 81.6%となります。
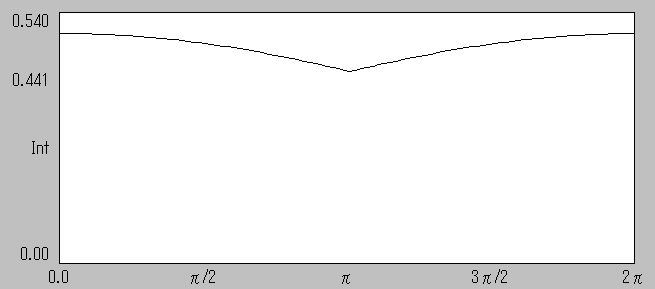
hamming

窓関数 BLACKMAN の場合　ピークの最大値を100%とすると最小値は 88.1%となります。
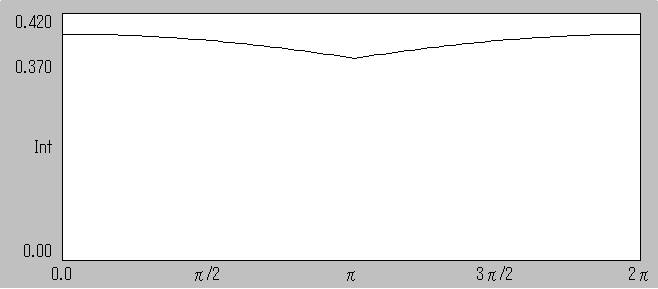
blackman

窓関数 TRIANGLE の場合　ピークの最大値を100%とすると最小値は 81%となります。
triangle

重ね合わせた場合
window-phase

結論
　演算窓の左端と右端の位相が１８０度の場合のピークの落ち込みが最も少ないのは 窓関数 Blackman でした。
　よって、定量性を議論する場合は 窓関数　Blackman を用いるのが良いと思われます。

前へ 次へ